3969. Дипломы

Когда Петя учился в школе, он часто участвовал в олимпиадах по информатике, математике и физике. Так как он был достаточно способным мальчиком и усердно учился, то на многих из этих олимпиад он получал дипломы. К окончанию школы у него накопилось n дипломов, причём, как оказалось, все они имели одинаковые размеры: w в ширину и h в высоту.

Сейчас Петя учится в одном из лучших университетов и живёт в общежитии со своими одногруппниками. Он решил украсить свою комнату, повесив на одну из стен свои дипломы за школьные олимпиады. Так как к бетонной стене прикрепить дипломы достаточно трудно, он решил купить специальную доску из пробкового дерева, чтобы прикрепить её к стене, а к ней – дипломы. Для того, чтобы эта конструкция выглядела более красиво, Петя хочет, чтобы она была квадратной и занимала как можно меньше места на стене. Каждый диплом должен быть размещён строго в прямоугольнике w на h. Дипломы запрещается поворачивать на 90 градусов. Прямоугольники, соответствующие различным дипломам, не должны иметь общих внутренних точек.

Напишите программу, которая вычислит минимальный размер стороны квадратной доски, которая потребуется Пете для размещения всех своих дипломов.

Вход. Три целых числа w, h, n (1 ≤ w, h, n ≤ 10⁹).

Выход. Выведите искомый минимальный размер стороны квадратной доски.

Пример входа	Пример выхода
2 3 10	9

РЕШЕНИЕ

бинарный поиск

Анализ алгоритма

Пусть x – искомая длина стороны квадратной доски. Будем искать x бинарным поиском. Очевидно, что 0 < x ≤ max(w, h) * n. Поиск начнем на отрезке [a; b] = [0; max(w, h) * n].

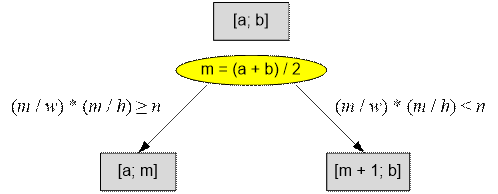
Пусть m = (a + b) / 2 – текущая длина стороны доски. Поскольку диплом имеет размер w * h, то на ней можно разместить максимум (m / w) * (m / h) дипломов. Если это число меньше n, то размер доски маловат, устанавливаем a = m + 1. Иначе двигаем правую границу поиска: b = m.

Пусть размер диплома w * h = 2 * 3.

· На доске 8 * 8 можно расположить максимум

(8 / 2) * (8 / 3) = 4 * 2 = 8 дипломов

· На доске 9 * 9 можно расположить максимум

(9 / 2) * (9 / 3) = 4 * 3 = 12 дипломов

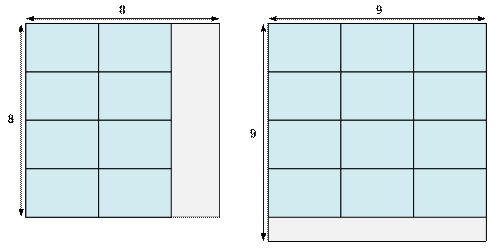
Минимальный размер стороны доски, на которой можно расположить 10 дипломов, равен 9.

Реализация алгоритма

Читаем входные данные.

scanf("%lld %lld %lld", &w, &h, &n);

Устанавливаем границы бинарного поиска [a; b] = [0; max(w, h) * n].

a = 0;

b = max(w, h) * n;

Запускаем бинарный поиск.

while (a < b)

{

m = (a + b) / 2;

Наибольшее количество дипломов размера w * h, которое можно расположить на доске со стороной m, равно dip = (m / w) * (m / h).

dip = (m / w) * (m / h);

if (dip < n) a = m + 1;

else b = m;

}

Выводим ответ.

printf("%lld\n", b);

Python реализация

Читаем входные данные.

w, h, n = map(int, input().split())

Устанавливаем границы бинарного поиска [a; b] = [0; max(w, h) * n].

a = 0

b = max(w, h) * n

Запускаем бинарный поиск.

while a < b:

m = (a + b) // 2

Наибольшее количество дипломов размера w * h, которое можно расположить на доске со стороной m, равно dip = (m / w) * (m / h).

dip = (m // w) * (m // h)

if dip < n:

a = m + 1

else:

b = m

Выводим ответ.

print(b)